Lösungen Band II, Vorlesung 5

Aufgabe 5.1

Beweisen Sie diese Behauptung.

Lösung:

Zu zeigen ist, dass jede hermitesche 2×2-Matrix $\textbf{L}$ in folgender Form geschrieben werden kann:

$\textbf{L} = a \sigma_x + b \sigma_y + c \sigma_z + d \textbf{I}.$

Wir wissen, dass eine hermitesche Matrix die Form

$\textbf{L} = \begin{pmatrix} r & w \\ w^* &r'\end{pmatrix}$

hat, wobei $r$ und $r'$ reell sind und $w$ komplex ist. Es muss also gelten:

$\begin{pmatrix} r & w \\ w^* &r'\end{pmatrix} = \begin{pmatrix} 0 & a\\ a & 0 \end{pmatrix} +\begin{pmatrix} 0 & -ib\\ ib & 0 \end{pmatrix} +\begin{pmatrix} c & 0\\ 0 & -c \end{pmatrix}+\begin{pmatrix} d & 0\\ 0 &d \end{pmatrix}= \begin{pmatrix} c+d & a-ib\\ a+ib & d-c\end{pmatrix}.$

Setzen wir

$a = Re(w), b = -Im(w), c = \frac{r-r'}{2}, d = \frac{r + r'}{2},$

so haben wir unsere Darstellung gefunden.

Aufgabe 5.2

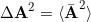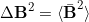Zeigen Sie, dass $\Delta \textbf{A}^2 = \braket{\bar{\textbf{A}}^2}$ und $\Delta \textbf{B}^2 = \braket{\bar{\textbf{B}}^2}$ gilt.
Zeigen Sie, dass $[\bar{\textbf{A}},\bar{\textbf{B}}] = [\textbf{A},\textbf{B}]$ gilt.
Zeigen Sie mit diesen Relationen, dass gilt:
$\Delta \textbf{A} \, \Delta \textbf{B} \ge \frac{1}{2} |\braket{\Psi|[\textbf{A},\textbf{B}]|\Psi}|.$

Lösung:

Die Aufgabe wurde teilweise schon in Abschnitt 5.4 auf S. 92f bewiesen.

1) Wir zeigen zuerst: Sind $\lambda_i$ die Eigenwerte von $\textbf{A}$ mit Eigenvektoren $\ket{\lambda_i}$ , so sind $\bar{\lambda}_i = \lambda_i - \braket{\textbf{A}}$ die Eigenwerte von $\bar{\textbf{A}}$ mit denselben Eigenvektoren $\ket{\lambda_i}$ :

$\bar{\textbf{A}} \ket{\lambda_i} = (\textbf{A}-\braket{\textbf{A}}) \ket{\lambda_i} = \textbf{A}\ket{\lambda_i} - \braket{\textbf{A}}\ket{\lambda_i} = \lambda_i\ket{\lambda_i} - \braket{\textbf{A}}\ket{\lambda_i} = (\lambda_i-\braket{\textbf{A}}) \ket{\lambda_i} = \bar{\lambda}_i \ket{\lambda_i}.$

Damit ist nach Definition von $\Delta \textbf{A}$

$(\Delta \textbf{A})^2 = \sum_i (\lambda_i - \braket{\textbf{A}})^2 P(\lambda_i) = \sum_i \bar{\lambda}_i P(\lambda_i) = \sum_i \bar{\lambda}_i P(\bar{\lambda}_i)= \braket{\bar{\textbf{A}}^2}.$

Dabei haben wir ausgenutzt, dass $P(\lambda_i) = P(\bar{\lambda}_i)$ gilt, da die gesamte Verteilung um $\braket{\textbf{A}}$ verschoben wurde.

Derselbe Beweis gilt natürlich auch für $\textbf{B}$ .

2) Es ist

$\begin{align*}[\bar{\textbf{A}},\bar{\textbf{B}}] &= \bar{\textbf{A}}\bar{\textbf{B}} - \bar{\textbf{B}}\bar{\textbf{A}} \\&= \big(\textbf{A}-\braket{\textbf{A}}\big) \big(\textbf{B}-\braket{\textbf{B}}\big) - \big(\textbf{B}-\braket{\textbf{B}}\big) \big(\textbf{A}-\braket{\textbf{A}}\big) \\&= \big( \textbf{A}\textbf{B} - \textbf{A}\braket{\textbf{B}}- \braket{\textbf{A}}\textbf{B}+ \braket{\textbf{A}}\braket{\textbf{B}} \big)- \big( \textbf{B}\textbf{A} - \textbf{B}\braket{\textbf{A}}- \braket{\textbf{B}}\textbf{A}+ \braket{\textbf{B}}\braket{\textbf{A}} \big)\\&= \textbf{A}\textbf{B} - \textbf{B}\textbf{A} \\&= [\textbf{A},\textbf{B}].\end{align*}$

Dabei ist zu beachten, dass $\braket{\textbf{A}}$ und $\braket{\textbf{B}}$ reelle Zahlen sind und damit z.B. $\textbf{A}\braket{\textbf{B}} =\braket{\textbf{B}}\textbf{A}$ gilt.

3) Schließlich gilt:

$\Delta \textbf{A} \Delta \textbf{B} = \Delta \bar{\textbf{A}} \Delta \bar{\textbf{B}} \ge \frac{1}{2} \braket{\Psi | [\bar{\textbf{A}},\bar{\textbf{B}} ]|\Psi} = \frac{1}{2} \braket{\Psi | [\textbf{A},\textbf{B} ]|\Psi}.$

Aufgabe 5.1

Lösung:

Aufgabe 5.2

Lösung:

Hinterlasse einen Kommentar. Antworten abbrechen