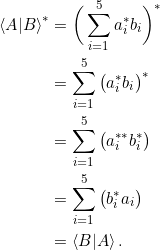Aufgabe 1.1
a) Beweisen Sie mit Hilfe der Axiome für innere Produkte:
![]()
b) Beweisen Sie:
Lösung:
a) Es gilt
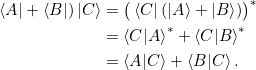
b) Da ![]() ist, gilt
ist, gilt ![]() , d.h. der Imaginärteil von
, d.h. der Imaginärteil von ![]() muss 0 sein und
muss 0 sein und ![]() damit reell.
damit reell.
Aufgabe 1.2
Zeigen Sie, dass das in Gl. 1.2 definierte Produkt die Axiome für innere Produkte erfüllt.
Lösung:
In Gl. 1.2 wird ein Skalarprodukt durch
![Rendered by QuickLaTeX.com \[ \braket{B|A} = \sum_{i=1}^5 b_i^* a_i\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-80958ad33821e317cb77e3d631f86d9f_l3.png)
definiert. Wir müssen die Linearität in der zweiten Komponente und die Antisymmetrie beweisen.
Linearität:
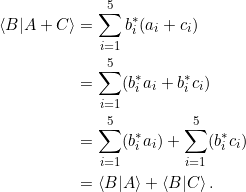
Antisymmetrie: