Aufgabe 8.1
Zeigen Sie, dass 
und 
lineare Operatoren sind.
Lösung:
Der Ortsoperator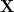
Der Ortsoperator ist einfach als Multiplikation mit der Koordinate 
definiert: 
Es gilt also für zwei Wellenfunktionen
![\[ \textbf{X}(\psi + \phi)(x) = x (\psi + \phi)(x) = x\psi(x) + x\phi(x) = \textbf{X}\psi(x) + \textbf{X}\phi(x), \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-12dda8118d08e02ca75e0a8c003b3c74_l3.png "Rendered by QuickLaTeX.com")
und für eine komplexe Konstante
![\[ \textbf{X}(z(\psi)(x)) = x(z\psi(x)) = z (x\psi(x)) = z(\textbf{X}\psi(x)).\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-d691e6264707fcc154ec16d49c1f2b34_l3.png "Rendered by QuickLaTeX.com")
Der Ortsoperator ist linear.
Der Differentialoperator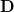
Der Differentialoperator ist als Ableitung nach der definiert: 
Für zwei Wellenfunktionen gilt damit
![\[ \textbf{D}(\psi + \phi)(x) = \frac{d(\psi + \phi)}{dx}(x) = \frac{d\psi }{dx}(x) + \frac{d\phi}{dx}(x) = \textbf{D}\psi(x) +\textbf{D}\phi(x),\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-bcf143854a0f301ba3969fb3b3e001da_l3.png "Rendered by QuickLaTeX.com")
und für eine komplexe Konstante
![\[ \textbf{D}(z(\psi)(x)) = \frac{dz\psi }{dx}(x) = z\frac{d\psi }{dx}(x) = z(\textbf{D}\psi(x)).\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-90ef0c9a629a9918c237770af5c6fd67_l3.png "Rendered by QuickLaTeX.com")
Der Differentialoperator ist linear.