Aufgabe 10.1
Ermitteln Sie die zweite Zeitableitung von ![]() in Gl 10.9 und zeigen Sie so, dass sie Gl. 10.8 erfüllt.
in Gl 10.9 und zeigen Sie so, dass sie Gl. 10.8 erfüllt.
Lösung:
Die zweite Ableitung lautet:
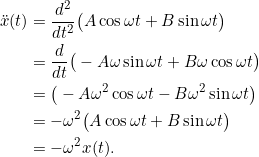
Ermitteln Sie die zweite Zeitableitung von ![]() in Gl 10.9 und zeigen Sie so, dass sie Gl. 10.8 erfüllt.
in Gl 10.9 und zeigen Sie so, dass sie Gl. 10.8 erfüllt.
Die zweite Ableitung lautet: