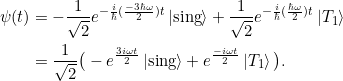Aufgabe 6.1
Zeigen Sie: Faktorisiert ![]() , so ist die Korrelation zwischen
, so ist die Korrelation zwischen ![]() und
und ![]() gleich 0.
gleich 0.
Lösung:
Sind ![]() und
und ![]() zwei Observablen, so lauten die Erwartungswerte
zwei Observablen, so lauten die Erwartungswerte
![]()
wobei die Summen über alle Eigenwerte ![]() bzw.
bzw. ![]() der Observablen gebildet werden. Für das Produkt der Erwartungswerte gilt dann:
der Observablen gebildet werden. Für das Produkt der Erwartungswerte gilt dann:
![]()
Dabei wird die letzte Summe über alle Kombinationen der ![]() und
und ![]() gebildet. Faktorisiert nun
gebildet. Faktorisiert nun ![]() , d.h. gilt
, d.h. gilt ![]() , so ist
, so ist
![]()
Das Mittelwert des Produkts ist in diesem Fall also das Produkt der Mittelwerte, d.h. ![]() .
.
Aufgabe 6.2
Zeigen Sie: Sind die beiden Normierungsbedingungen aus Gl. 6.4 erfüllt, so ist der Zustandsvektor aus Gl. 6.5 ebenfalls automatisch normiert. Mit anderen Worten sollen Sie zeigen, dass aus der Normierung des gesamten Zustandsvektors keine zusätzlichen Einschränkungen an die ![]() und
und ![]() folgen.
folgen.
Lösung:
Wir haben die beiden Zustände ![]() und
und ![]() mit den Normierungsbedingungen
mit den Normierungsbedingungen
![]()
Der Produktzustand lautet
![]()
und hat die Norm
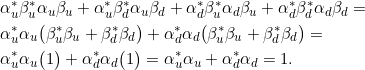
Also ist der Produktzustand zweier normierter Zustände ebenfalls normiert.
(Beachte, dass die ![]() und
und ![]() einfach komplexe Zahlen sind, und wir ganz normal damit rechnen können.)
einfach komplexe Zahlen sind, und wir ganz normal damit rechnen können.)
Aufgabe 6.3
Zeigen Sie, dass der Zustand ![]() nicht als Produktzustand geschrieben werden kann.
nicht als Produktzustand geschrieben werden kann.
Lösung:
Versuchen wir einmal, ![]() als Produktzustand zu schreiben, also in der Form
als Produktzustand zu schreiben, also in der Form
![]()
Wir lesen direkt ab, dass
![]()
gelten muss, und dass dann
![]()
ist. Aus den beiden lezten Gleichungen folgt, dass
Eine einfache Knobelaufgabe, keine große Mathematik!
Aufgabe 6.4
Benutzen Sie die Matrixdarstellungen von ![]() ,
, ![]() und
und ![]() und die Spaltenvektoren für
und die Spaltenvektoren für ![]() und
und ![]() , um Gl. 6.6 zu überprüfen. Verwenden Sie dann Gl. 6.6 und Gl. 6.7, um die fehlenden Gleichungen in Gl. 6.8 zu bestimmen. Sehen Sie im Anhang nach, ob ihre Antworten richtig sind.
, um Gl. 6.6 zu überprüfen. Verwenden Sie dann Gl. 6.6 und Gl. 6.7, um die fehlenden Gleichungen in Gl. 6.8 zu bestimmen. Sehen Sie im Anhang nach, ob ihre Antworten richtig sind.
Lösung:
Hier kommen die Berechnungen zu Gl. 6.6:
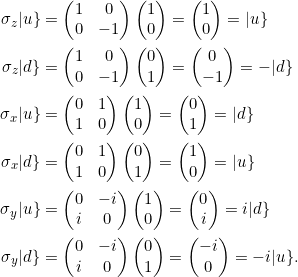
Der zweite Teil der Aufgabe bringt nicht viele Erkenntnisse. Die Lösung besteht einfach darin, bei Anwendung von Alice ![]() -Operatoren den ersten Buchstaben im Ket-Vektor gemäß Gleichungen 6.6 auszutauschen, und bei Bobs
-Operatoren den ersten Buchstaben im Ket-Vektor gemäß Gleichungen 6.6 auszutauschen, und bei Bobs ![]() -Operatoren den zweiten (incl. Vorzeichenwechsel und Multiplikation mit
-Operatoren den zweiten (incl. Vorzeichenwechsel und Multiplikation mit ![]() ). Ich mache das einmal für Alices Operator:
). Ich mache das einmal für Alices Operator:
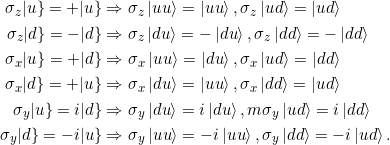
Ganz genauso geht das für Bobs Operator, nur ändert sich hier der \textit{zweite} Buchstabe im Produktzustand:
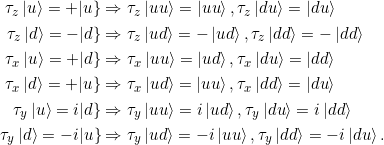
Aufgabe 6.5
Beweisen Sie den folgenden Satz:
Wenn irgendeiner von Alices oder Bobs Spinoperatoren auf einen Produktzustand wirkt, so ist das Ergebnis wieder ein Produktzustand.
Zeigen Sie, dass in einem Produktzustand der Erwartungswert jeder Komponente von ![]() oder
oder ![]() genau derselbe ist wie im individuellen Einzel-Spin-Zustand.
genau derselbe ist wie im individuellen Einzel-Spin-Zustand.
Lösung:
Den Satz haben wir bereits in Aufgabe 6.4 bewiesen, denn wir haben die Operatoren auf alle Basis-Produktzustände angewandt und wieder Produktzustände erhalten. Wegen der Linearität der Operatoren folgt dies nun für alle möglichen Produktzustände.
Allgemein gilt: Ist ![]() einer von Alices Spin-Operatoren mit
einer von Alices Spin-Operatoren mit ![]() , und ist
, und ist ![]() ein Produktzustand, so gilt:
ein Produktzustand, so gilt:
![]()
Analog für Bobs Spin-Operatoren:
![]()
Wir können dies auch noch ausführlich nachrechnen. Betrachten wir den allgemeinen Produktzustand
![]()
Dann gilt:
![Rendered by QuickLaTeX.com \begin{align*} \big(\sigma_z \otimes \Id \big) \ket{ab} &= \big[ \big(\sigma_z \otimes \Id \big) \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\big]\\ &= \sigma_z \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \Id \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\\ &= \big(\alpha_u \sigma_z \keta{u} + \alpha_d \sigma_z \keta{d}\big) \otimes \big(\beta_u \Id\ket{u} + \beta_d \Id \ket{d}\big)\\ &= \big(\alpha_u \keta{u} - \alpha_d \keta{d}\big) \otimes \big(\beta_u \ket{u} + \beta_d \ket{d}\big), \end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-f53da9d4e4e755e2269193f078c820af_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \big(\sigma_x \otimes \Id \big) \ket{ab} &= \big[ \big(\sigma_x \otimes \Id \big) \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\big]\\&= \sigma_x \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \Id \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\\ &= \big(\alpha_u \sigma_x \keta{u} + \alpha_d \sigma_x \keta{d}\big) \otimes \big(\beta_u \Id\ket{u} + \beta_d \Id \ket{d}\big)\\&= \big(\alpha_u \keta{d} + \alpha_d \keta{u}\big) \otimes \big(\beta_u \ket{u} + \beta_d \ket{d}\big), \end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-62925a9b116ea1cad7f01e7988cc3946_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \big(\sigma_y \otimes \Id \big) \ket{ab} &= \big[ \big(\sigma_y \otimes \Id \big) \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\big]\\ &= \sigma_y \big(\alpha_u\keta{u} + \alpha_d \keta{d}\big) \otimes \Id \big(\beta_u\ket{u} + \beta_d \ket{d}\big)\\ &= \big(\alpha_u \sigma_y \keta{u} + \alpha_d \sigma_y \keta{d}\big) \otimes \big(\beta_u \Id\ket{u} + \beta_d \Id \ket{d}\big)\\ &= \big(\alpha_u i\keta{d} - \alpha_d i \keta{u}\big) \otimes \big(\beta_u \ket{u} + \beta_d \ket{d}\big). \end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-93e5649143fbf9b319bc5cf8fa79f0ca_l3.png)
Da die Spinoperatoren (wie alle Operatoren) linear sind, wirken sie letztlich nur auf die Basisvektoren, und die Produkt-Struktur der Zustandsvektoren bleibt erhalten. Die Spinoperatoren bilden Produktzustände auf Produktzustände ab.
Für die Erwartungswerte gilt:
![Rendered by QuickLaTeX.com \begin{align*} \braket{\sigma_z} &= \braket{ab|\sigma_z | ab}\\ &= \bra{ab} \sigma_z \big[ \alpha_u \beta_u \ket{uu} + \alpha_u \beta_d \ket{ud} + \alpha_d \beta_u \ket{du} + \alpha_d \beta_d \ket{dd} \big]\\&= \bra{ab} \big[ \alpha_u \beta_u \ket{uu} + \alpha_u \beta_d \ket{ud} - \alpha_d \beta_u \ket{du} - \alpha_d \beta_d \ket{dd} \big] \\&= \big[ \alpha_u^* \beta_u^*\bra{uu} + \alpha_u^* \beta_d^*\bra{ud} + \alpha_d^* \beta_u^*\bra{du} + \alpha_d^* \beta_d^*\bra{dd} \big] \\&\phantom{=}\;\big[ \alpha_u \beta_u \ket{uu} + \alpha_u \beta_d \ket{ud} - \alpha_d \beta_u \ket{du} - \alpha_d \beta_d \ket{dd} \big] \\&= \alpha_u^* \beta_u^* \alpha_u \beta_u + \alpha_u^* \beta_d^* \alpha_u \beta_d - \alpha_d^* \beta_u^* \alpha_d \beta_u - \alpha_d^* \beta_d^* \alpha_d \beta_d \\&= (\beta_u^*\beta_u)(\alpha_u^*\alpha_u - \alpha_d^*\alpha_d ) + (\beta_d^*\beta_d)(\alpha_u^*\alpha_u - \alpha_d^*\alpha_d )\\&= (\beta_u^*\beta_u + \beta_d^*\beta_d)(\alpha_u^*\alpha_u - \alpha_d^*\alpha_d )\\&= \alpha_u^*\alpha_u - \alpha_d^*\alpha_d.\end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-1c21b6a1bfc6fec9592032590283b009_l3.png)
Dies ist genau der Erwartungswert für Alices Einzel-Spin:
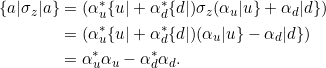
Nun zu den Erwartungswerten von ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*} \braket{\sigma_x} &= \braket{ab|\sigma_x | ab}\\ &= \bra{ab} \sigma_x \big[ \alpha_u \beta_u \ket{uu} + \alpha_u \beta_d \ket{ud} + \alpha_d \beta_u \ket{du} + \alpha_d \beta_d \ket{dd} \big]\\ &= \bra{ab} \big[ \alpha_u \beta_u \ket{du} + \alpha_u \beta_d \ket{dd} + \alpha_d \beta_u \ket{uu} + \alpha_d \beta_d \ket{ud} \big] \\ &= \big[ \alpha_u^* \beta_u^*\bra{uu} + \alpha_u^* \beta_d^*\bra{ud} + \alpha_d^* \beta_u^*\bra{du} + \alpha_d^* \beta_d^*\bra{dd} \big] \\ &\phantom{=}\;\big[ \alpha_u \beta_u \ket{du} + \alpha_u \beta_d \ket{dd} + \alpha_d \beta_u \ket{uu} + \alpha_d \beta_d \ket{ud} \big] \\ &= \alpha_u^* \beta_u^* \alpha_d \beta_u + \alpha_u^* \beta_d^* \alpha_d \beta_d + \alpha_d^* \beta_u^* \alpha_u \beta_u + \alpha_d^* \beta_d^* \alpha_u \beta_d \\&= (\beta_u^*\beta_u)(\alpha_u^*\alpha_d + \alpha_d^*\alpha_u ) + (\beta_d^*\beta_d)(\alpha_u^*\alpha_d + \alpha_d^*\alpha_u )\\&= (\beta_u^*\beta_u + \beta_d^*\beta_d)(\alpha_u^*\alpha_d + \alpha_d^*\alpha_u )\\&= \alpha_u^*\alpha_d + \alpha_d^*\alpha_u.\end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-7f1a49afa4f8e895dbb1c2108fbd0dfb_l3.png)
Dies ist der Erwartungswert für Alices Einzel-Spin:
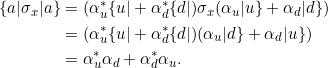
Schließlich gilt für die Erwartungswerte von ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}\braket{\sigma_y} &= \braket{ab|\sigma_y | ab}\\&= \bra{ab} \sigma_y \big[ \alpha_u \beta_u \ket{uu} + \alpha_u \beta_d \ket{ud} + \alpha_d \beta_u \ket{du} + \alpha_d \beta_d \ket{dd} \big]\\&= \bra{ab} \big[ \alpha_u \beta_u i\ket{du} + \alpha_u \beta_d i\ket{dd} - \alpha_d \beta_u i\ket{uu} - \alpha_d \beta_d i\ket{ud} \big] \\&= \big[ \alpha_u^* \beta_u^*\bra{uu} + \alpha_u^* \beta_d^*\bra{ud} + \alpha_d^* \beta_u^*\bra{du} + \alpha_d^* \beta_d^*\bra{dd} \big] \\ &\phantom{=}\;\big[ \alpha_u \beta_u i\ket{du} + \alpha_u \beta_d i\ket{dd} - \alpha_d \beta_u i\ket{uu} - \alpha_d \beta_d i\ket{ud} \big] \\ &= -i\alpha_u^* \beta_u^* \alpha_d \beta_u - i\alpha_u^* \beta_d^* \alpha_d \beta_d + i\alpha_d^* \beta_u^* \alpha_u \beta_u + i\alpha_d^* \beta_d^* \alpha_u \beta_d \\&= i(\beta_u^*\beta_u)(-\alpha_u^*\alpha_d + \alpha_d^*\alpha_u ) + i(\beta_d^*\beta_d)(-\alpha_u^*\alpha_d + \alpha_d^*\alpha_u )\\&= (\beta_u^*\beta_u + \beta_d^*\beta_d)(-\alpha_u^*\alpha_d + \alpha_d^*\alpha_u )\\&= -i\alpha_u^*\alpha_d + i\alpha_d^*\alpha_u.\end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-1e541b77775b0eae543e0fa9660fc5bb_l3.png)
Dies ist der Erwartungswert für Alices Einzel-Spin:
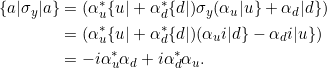
Die Erwartungswerte stimmen also jeweils überein.
Die Rechnungen für Bobs ![]() -Operatoren gehen natürlich ganz genau so, und ich erspare sie mir/uns.
-Operatoren gehen natürlich ganz genau so, und ich erspare sie mir/uns.
Aufgabe 6.6
Nehmen Sie an, dass Charlie die beiden Spins im Singulett-Zustand präpariert hat. Dieses Mal misst Bob ![]() und Alice
und Alice ![]() . Was ist der Erwartungswert von
. Was ist der Erwartungswert von ![]() ?
?
Was sagt das über die Korrelation zwischen den beiden Messungen aus?
Lösung:
Wir wissen bereits (S. 114), dass die Erwartungswerte ![]() und
und ![]() gleich 0 sind.
gleich 0 sind.
Wir berechnen nun den Erwartungswert ![]() :
:
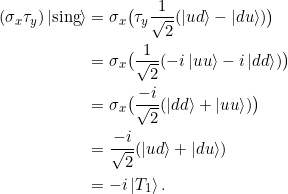
Es gilt:
![]()
und damit
![]()
Die Erwartungswerte ![]() ,
, ![]() und
und ![]() sind also alle 0, und damit gilt auch
sind also alle 0, und damit gilt auch ![]() . Die Messungen sind völlig unkorreliert.
. Die Messungen sind völlig unkorreliert.
Aufgabe 6.7
Als Nächstes präpariert Charlie die Spins in einem anderen Zustand namens ![]() , wobei
, wobei
![]()
In diesen Beispielen steht ![]() für Triplett. Diese Triplett-Zustände sind grundverschieden von den Zuständen mit den Beispielen mit Münzen und Würfeln.
für Triplett. Diese Triplett-Zustände sind grundverschieden von den Zuständen mit den Beispielen mit Münzen und Würfeln.
Was sind die Erwartungswerte der Operatoren ![]() ,
, ![]() und
und ![]() ?
?
Was für einen Unterschied so ein Vorzeichen machen kann!
Lösung:
Es ist
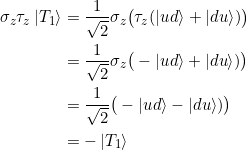
und damit
![]()
Es gilt weiter
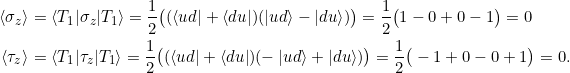
Damit beträgt die Korrelation zwischen ![]() und
und ![]() :
: ![]()
Weiter ist
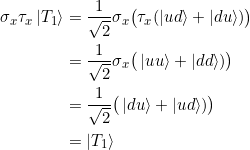
und damit
![]()
Wieder gilt

und damit ![]()
Schließlich gilt
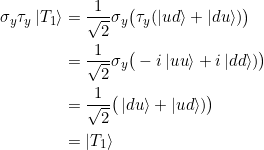
und damit
![]()
Wieder gilt
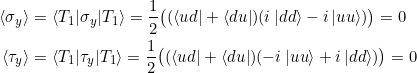
und damit ![]()
Die Erwartungswerte der zusammengesetzten Operatoren sind also ![]() bzw.
bzw. ![]() , und die Operatoren sind jeweils vollständig korreliert.
, und die Operatoren sind jeweils vollständig korreliert.
Aufgabe 6.8
Machen Sie dasselbe für die beiden verschränkten Triplett-Zustände
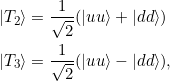
und interpretieren Sie das Ergebnis.
Lösung:
Das wird jetzt eine echte Fleißarbeit; die ganze Rechnung läuft wie in Aufgabe 6.7. Wir bemerken aber: ![]() und
und ![]() sind von der Form
sind von der Form ![]() , d.h. der erste und zweite Buchstabe in den beiden Kets sind gleich, nur das Vorzeichen dazwischen ist anders. Daher wirken die
, d.h. der erste und zweite Buchstabe in den beiden Kets sind gleich, nur das Vorzeichen dazwischen ist anders. Daher wirken die ![]() und
und ![]() auf
auf ![]() und
und ![]() gleich, und die Erwartungswerte der
gleich, und die Erwartungswerte der ![]() und
und ![]() sind ebenfalls gleich.
sind ebenfalls gleich.
Wir beginnen mit 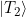 :
:
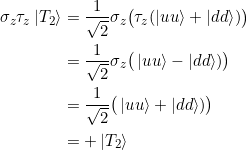
und damit
![]()
Die Erwartungswerte der einzelnen Operatoren stimmen, wie bereits erwähnt, überein:
![]()
Damit beträgt die Korrelation zwischen ![]() und
und ![]() :
: ![]()
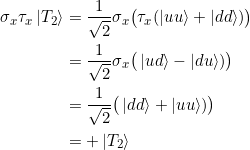
und damit
![]()
Es gilt weiter
![]()
Damit beträgt die Korrelation zwischen ![]() und
und ![]() :
: ![]()
Schließlich ist
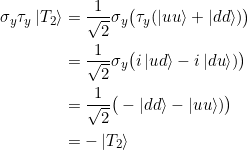
und damit
![]()
Es gilt weiter
![]()
Damit beträgt die Korrelation zwischen ![]() und
und ![]() :
: ![]()
Die ganze Rechnung noch einmal mit  :
:
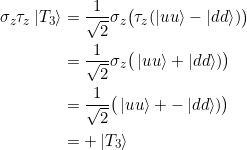
und damit
![]()
Die Erwartungswerte der einzelnen Operatoren stimmen, wie bereits erwähnt, überein:
![]()

und damit
![]()
Es gilt weiter
![]()
![]()
und damit
![]()
Es gilt weiter
![]()
Zusammenfassung
![]() und
und ![]() sind Eigenvektoren von
sind Eigenvektoren von ![]()
![]() und
und ![]() zu den Eigenwerten
zu den Eigenwerten ![]() und
und ![]()
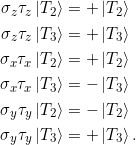
Entsprechend gilt für die Erwartungswerte:
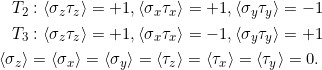
Damit liegt jeweils maximale Korrelation vor.
Aufgabe 6.9
Beweisen Sie, dass die vier Vektoren ![]() ,
, ![]() ,
, ![]() und
und ![]() Eigenvektoren von
Eigenvektoren von ![]() sind. Wie lauten ihre Eigenwerte?
sind. Wie lauten ihre Eigenwerte?
Lösung:
Einen großen Teil der Arbeit haben wir bereits in den Aufgaben 6.7 und 6.8 erledigt. Wir greifen jetzt auf die Ergebnisse zurück:
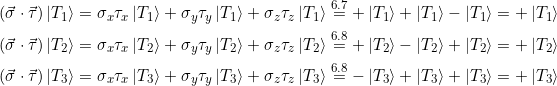
Die Triplett-Zustände sind also drei Eigenvektoren zum (dreifach entarteten) Eigenwert +1.
Wir müssen die Berechnungen noch für ![]() nachholen:
nachholen:
![]()
![]()
![]()
Daher gilt
![]()
![]() ist also Eigenvektor von
ist also Eigenvektor von ![]() zum Eigenwert -3.
zum Eigenwert -3.
Aufgabe 6.10
Ein System mit zwei Spins hat die Hamilton-Funktion
![]()
Was sind die möglichen Energien des Systems, und was sind die Eigenvektoren der Hamilton-Funktion?
Nehmen Sie an, das System startet im Zustand ![]() . Was ist der Zustand zu einem späteren Zeitpunkt? Beantworten Sie diese Frage auch für die Anfangszustände
. Was ist der Zustand zu einem späteren Zeitpunkt? Beantworten Sie diese Frage auch für die Anfangszustände ![]() ,
, ![]() und
und ![]()
Lösung:
In Aufgabe 6.9 haben wir gesehen, dass der Singulett- und die Triplett-Zustände die Eigenvektoren von ![]() sind zu den Eigenwerten
sind zu den Eigenwerten ![]() bzw.
bzw. ![]()
Dadurch lesen wir aus der zeitunabhängigen Schrödingergleichung
![]()
direkt die Energieeigenwerte ab, denn es ist
![]()
und
![]()
(für k=1,2,3). Die Energieeigenwerte sind ![]() und
und ![]() , und
, und ![]() bilden eine Orthonormalbasis aus Energieeigenvektoren.
bilden eine Orthonormalbasis aus Energieeigenvektoren.
Man sieht leicht:
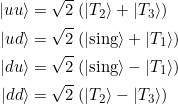
Im zweiten Teil der Aufgabe gehen wir gemäß dem „Rezepts für ein Schrödinger-Ketzchen“ vor (Kasten auf S. 81). Dazu bilden wir die Produkte ![]() der eben bestimmten Energieeigenvektoren
der eben bestimmten Energieeigenvektoren ![]() mit dem Startzustand
mit dem Startzustand ![]() und erhalten daraus die gewünschte Darstellung:
und erhalten daraus die gewünschte Darstellung:
![]()
Die Koeffizienten ![]() sind 0 für
sind 0 für ![]() und
und ![]() , da diese Zustände nur
, da diese Zustände nur ![]() und
und ![]() als Komponenten enthalten. Weiter ist
als Komponenten enthalten. Weiter ist
![]()
Der Eigenwert ist beide Male ![]() , und somit folgt
, und somit folgt
![]()
Ganz genauso geht die Rechnung für den Startzustand ![]() :
:
Die Koeffizienten ![]() sind wieder gleich 0 für
sind wieder gleich 0 für ![]() und
und ![]() , und es ist
, und es ist
![]()
Der Eigenwert ist beide Male ![]() , und somit folgt
, und somit folgt
![]()
Die zeitliche Entwicklung von ![]() und
und ![]() macht sich also nur in der Änderung der Phase bemerkbar, denn
macht sich also nur in der Änderung der Phase bemerkbar, denn ![]() ist ein Phasenfaktor.
ist ein Phasenfaktor.
Bei den Startzuständen ![]() und
und ![]() sind nun umgekehrt die Skalarprodukte mit
sind nun umgekehrt die Skalarprodukte mit ![]() und
und ![]() gleich 0, so dass wir nur die Koeffizienten für
gleich 0, so dass wir nur die Koeffizienten für ![]() und
und ![]() berechnen müssen:
berechnen müssen:
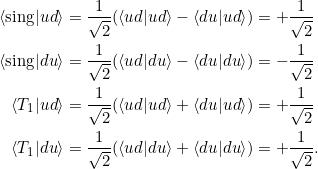
Damit gilt für ![]() :
:
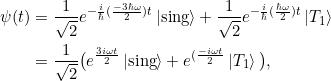
und für ![]()