Aufgabe 7.1
Schreiben Sie das Tensorprodukt ![]() als Matrix, und wenden Sie die Matrix an auf jeden der Spaltenvektoren
als Matrix, und wenden Sie die Matrix an auf jeden der Spaltenvektoren ![]() ,
, ![]() ,
, ![]() und
und ![]() . Zeigen Sie, dass Alices Hälfte des Zustandsvektors in jedem Fall unverändert bleibt. Dabei ist
. Zeigen Sie, dass Alices Hälfte des Zustandsvektors in jedem Fall unverändert bleibt. Dabei ist ![]() wieder die
wieder die ![]() -Einheitsmatrix.
-Einheitsmatrix.
Lösung:
![]() ist eine
ist eine ![]() -Matrix. Wir gehen vor wie im Abschnitt 7.1.1 beschrieben:
-Matrix. Wir gehen vor wie im Abschnitt 7.1.1 beschrieben:
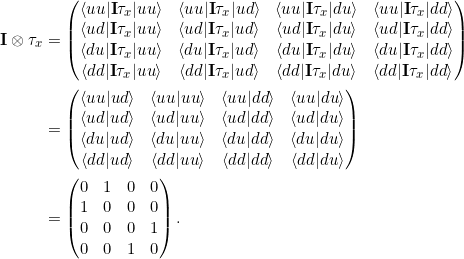
Das ist nun unsere Tensorprodukt-Matrix. Sie vertauscht also jeweils die ersten beiden und die letzten Einträge eines Zustandsvektors. Wir wissen aus Gl 7.9:
![Rendered by QuickLaTeX.com \[\ket{uu} = \begin{pmatrix}1\\0\\0\\0 \end{pmatrix},\ket{ud} = \begin{pmatrix}0\\1\\0\\0 \end{pmatrix},\ket{du} = \begin{pmatrix}0\\0\\1\\0 \end{pmatrix},\ket{dd} = \begin{pmatrix}0\\0\\0\\1 \end{pmatrix}.\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-a7bedf30c530c456567137af742d909f_l3.png)
Damit ist (vertausche jeweils die ersten beiden und letzten beiden Komponenten des Zustandsvektors)

Wie man sieht, bleibt Alices (die erste Komponente) des Tensorprodukts erhalten, nur Bobs (die zweite) Komponente wechselt von ![]() nach
nach ![]() und umgekehrt.
und umgekehrt.
Aufgabe 7.2
Berechnen Sie die Matrixelemente von ![]() , indem Sie die inneren Produkte bilden, wie wir es in Gl. 7.2 getan haben.
, indem Sie die inneren Produkte bilden, wie wir es in Gl. 7.2 getan haben.
Lösung:
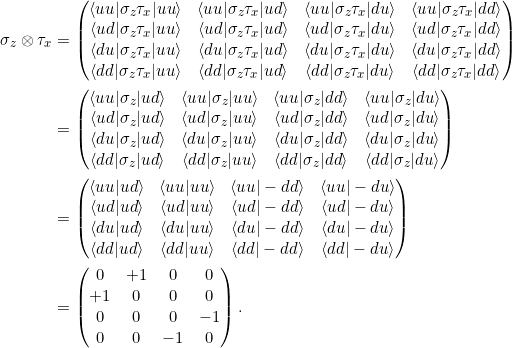
Aufgabe 7.3
a) Schreiben Sie Gl. 7.10 um in Komponentenform, indem Sie die Symbole ![]() ,
, ![]() ,
, ![]() und
und ![]() durch die Matrizen und Spaltenvektoren aus Gl. 7.7 und Gl. 7.8 ersetzen.
durch die Matrizen und Spaltenvektoren aus Gl. 7.7 und Gl. 7.8 ersetzen.
b) Führen Sie die Matrixmultiplikationen ![]() und
und ![]() auf der rechten Seite durch. Überprüfen Sie, dass jedes Ergebnis eine
auf der rechten Seite durch. Überprüfen Sie, dass jedes Ergebnis eine ![]() -Matrix ist.
-Matrix ist.
c) Schreiben Sie alle drei Kroneckerprodukte ausführlich hin.
d)Überprüfen Sie die Zeilen- und Spaltenzahlen aller Kroneckerprodukte:
e) Führen Sie die Matrixmultiplikation auf der linken Seite durch, was einen ![]() -Spaltenvektor ergibt. Jede Zeile sollte die Summe aus vier einzelnen Termen sein.
-Spaltenvektor ergibt. Jede Zeile sollte die Summe aus vier einzelnen Termen sein.
f) Überprüfen Sie schließlich, dass die erzeugten Spaltenvektoren auf der linken und rechten Seite übereinstimmen.
Lösung:
Es geht um die Gleichung 7.10:
![]()
wobei
a)
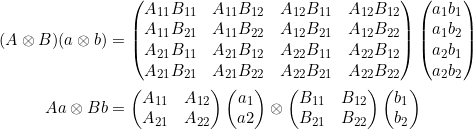
b)
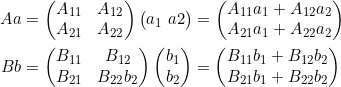
Wie man sieht, ist das Ergebnis eine ![]() -Matrix, sprich ein zweidimensionaler Vektor.
-Matrix, sprich ein zweidimensionaler Vektor.
c)
![Rendered by QuickLaTeX.com \[ A \otimes B = \begin{pmatrix}A_{11}B_{11} & A_{11} B_{12} & A_{12}B_{11} & A_{12} B_{12} \\A_{11}B_{21} & A_{11} B_{22} & A_{12}B_{21} & A_{12} B_{22} \\A_{21}B_{11} & A_{21} B_{12} & A_{22}B_{11} & A_{22} B_{12} \\A_{21}B_{21} & A_{21} B_{22} & A_{22}B_{21} & A_{22} B_{22}\end{pmatrix}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-6c413d18cb2cc058d3c8951f6b747ede_l3.png)
![Rendered by QuickLaTeX.com \[a\otimes b = \begin{pmatrix} a_1 b_1 \\ a_1 b_2 \\ a_2 b_1 \\ a_2 b_2 \end{pmatrix} \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-0403d611dc54783a897d663b3fcf5df2_l3.png)
![Rendered by QuickLaTeX.com \[ Aa \otimes Bb = \begin{pmatrix}(A_{11}a_1 + A_{12}a_2) (B_{11} b_1 + B_{12}b_2) \\(A_{11}a_1 + A_{12}a_2) (B_{21} b_1 + B_{22}b_2) \\(A_{21}a_1 + A_{22}a_2) (B_{11} b_1 + B_{12}b_2) \\(A_{21}a_1 + A_{22}a_2) (B_{21} b_1 + B_{22}b_2)\end{pmatrix} \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b277a82a7f36356aa6161b77ea35b5f3_l3.png)
d) ![]() ist tatsächlich eine
ist tatsächlich eine ![]() -Matrix, und
-Matrix, und ![]() und
und ![]() sind Vektoren der Dimension 4.
sind Vektoren der Dimension 4.
e)
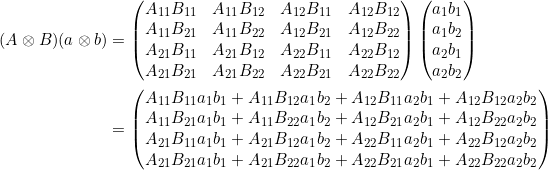
f) Vergleichen wir die letzten Terme in in c) und e) so sehen wir, dass sie durch Ausmultiplizieren bzw. Ausklammern ineinander übergehen. Die Gleichung ist also korrekt!
Wie man sieht, steckt hinter dem ![]() -Zeichen eine ganze Menge Rechnerei. Seien wir froh, dass es den Matrizenkalkül gibt, so dass wir nicht ständig mit den ganzen Komponenten rechnen müssen!
-Zeichen eine ganze Menge Rechnerei. Seien wir froh, dass es den Matrizenkalkül gibt, so dass wir nicht ständig mit den ganzen Komponenten rechnen müssen!
Aufgabe 7.4
Berechnen Sie die Dichtematrix für
![]()
Antwort:
![]()
![]()
Versuchen Sie nun, einige Zahlen in
Lösung:
Die Dichtematrix lautet
![]()
wobei sich ![]() und
und ![]() ergeben aus
ergeben aus
![]()
also ![]() und
und ![]() , und damit
, und damit
![]()
Wir können nun alle komplexen Zahlen ![]() und
und ![]() einsetzen, für die
einsetzen, für die ![]() gilt.
gilt.
Hier ein paar Beispiele:
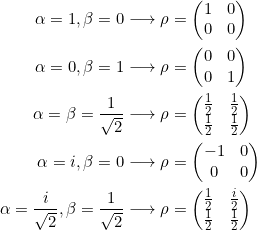
Aufgabe 7.5
a) Zeigen Sie
![]()
b) Nehmen Sie nun an, dass
![]()
ist. Berechnen Sie
c) Falls ![]() eine Dichtematrix ist, steht sie dann für einen reinen oder für einen gemischten Zustand?
eine Dichtematrix ist, steht sie dann für einen reinen oder für einen gemischten Zustand?
Lösung:
a)
![]()
b)
![]()
c) Ist ![]() eine Dichtematrix, so beschreibt
eine Dichtematrix, so beschreibt ![]() einen gemischten Zustand, denn es ist
einen gemischten Zustand, denn es ist ![]() und
und ![]() (s. Kasten S. 137).
(s. Kasten S. 137).
Aufgabe 7.6
Verwenden Sie Gl. 7.22, um zu zeigen: Ist ![]() eine Dichtematrix, so gilt
eine Dichtematrix, so gilt
![]()
Lösung:
Gl. 7.22 besagt ![]() , und da für die Summe aller Wahrscheinlichkeiten
, und da für die Summe aller Wahrscheinlichkeiten ![]() gelten muss, ist
gelten muss, ist
![]()
Aufgabe 7.7
Verwenden Sie Gl. 7.24, um ![]() zu berechnen. Wie bestätigt dieses Ergebnis, dass
zu berechnen. Wie bestätigt dieses Ergebnis, dass ![]() einen verschränkten Zustand darstellt? Wir werden bald feststellen, dass es noch andere Möglichkeiten gibt, Verschränkungen zu überprüfen.
einen verschränkten Zustand darstellt? Wir werden bald feststellen, dass es noch andere Möglichkeiten gibt, Verschränkungen zu überprüfen.
Lösung:
Da
![]()
ist, folgt, dass der beschriebene Zustand verschränkt ist. Dies folgt auch aus ![]()
Aufgabe 7.8
Betrachten Sie die folgenden Zustände:
Berechnen Sie für jeden Zustand Alices Dichtematrix und Bobs Dichtematrix. Untersuchen Sie deren Eigenschaften.
Lösung:
Wir gehen vor wie im Beispiel in 7.6 beschrieben.
![]() :
:
Es ist:
![]()
Es gilt daher nach Gl. 7.23 für Alices Dichtematrix:
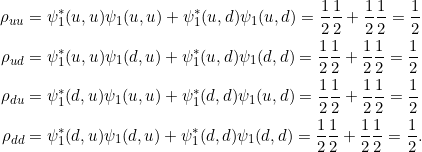
und damit
![]()
Wegen der „Symmetrie“ von ![]() in der ersten und zweiten Komponente ist dies auch die Dichtematrix von Bob. (Mit Symmetrie ist hier gemeint: Vertauscht man jeweils die erste und zweite Komponente in den Kets in der Summe, die
in der ersten und zweiten Komponente ist dies auch die Dichtematrix von Bob. (Mit Symmetrie ist hier gemeint: Vertauscht man jeweils die erste und zweite Komponente in den Kets in der Summe, die ![]() bildet, so erhält man wieder
bildet, so erhält man wieder ![]() .)
.)
Wir berechnen ![]() :
:
![]()
Der Zustand ![]() ist also unverschränkt, d.h. ein Produktzustand.
ist also unverschränkt, d.h. ein Produktzustand.
![]() :
:
Es ist
![]()
Es gilt daher nach Gl. 7.23 für Alices Dichtematrix:
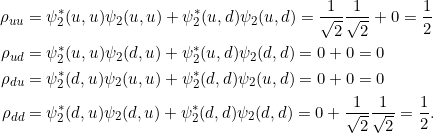
und damit
![]()
Dies ist auch wieder Bobs Dichtematrix, denn auch dieser Ausdruck ist symmetrisch in der ersten und zweiten Komponente. Wegen
![]()
ist der Zustand verschränkt, was uns nicht überraschen sollte, denn es handelt sich um einen der Triplett-Zustände, die wir in Abschnitt 6.7 über verschränkte Zustände kennengelernt haben.
![]() :
:
Es ist
![]()
Alices Dichtmatrix:
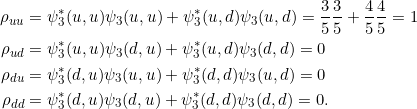
und damit
![]()
Da für die Dichtematrix gilt:
![]()
ist der Zustand unverschränkt.
Aber ![]() ist nicht Bobs Dichtematrix, denn man kann bei
ist nicht Bobs Dichtematrix, denn man kann bei ![]() nicht die ersten und zweiten Komponenten vertauschen. Wir müssen daher noch eine zweite Rechnung für Bobs Dichtematrix
nicht die ersten und zweiten Komponenten vertauschen. Wir müssen daher noch eine zweite Rechnung für Bobs Dichtematrix ![]() durchführen. Die Komponenten der Wellenfunktion
durchführen. Die Komponenten der Wellenfunktion ![]() sind dabei zwar identisch, denn Alice und Bob betrachten ja denselben Zustand in derselben Basis und arbeiten daher mit derselben Wellenfunktion. Ihre Dichtematrizen werden aber trotzdem unterschiedlich berechnet.
sind dabei zwar identisch, denn Alice und Bob betrachten ja denselben Zustand in derselben Basis und arbeiten daher mit derselben Wellenfunktion. Ihre Dichtematrizen werden aber trotzdem unterschiedlich berechnet.
So ist etwa Alices ![]() und Bobs
und Bobs ![]() .
.
Es ist
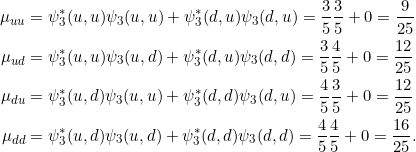
und damit
![]()
Es ist nun
![]()
Auch Bobs Dichtematrix zeigt, dass der Zustand unverschränkt ist. Alles andere hätte auf einen Fehler hingedeutet, denn wenn der Zustand für Alice unverschränkt ist, so ist er natürlich für alle anderen auch unverschränkt.
Aufgabe 7.9
Zeigen Sie für eine Observable ![]() von Alice und eine Observable
von Alice und eine Observable ![]() von Bob, dass für einen Produktzustand die Korrelation
von Bob, dass für einen Produktzustand die Korrelation ![]() 0 beträgt.
0 beträgt.
Lösung:
Wir müssen zeigen, dass für einen Produktzustand gilt: ![]() .
.
In einem Produktzustand faktorisiert die Wahrscheinlichkeit, d.h. es gilt
![]()
und damit gilt
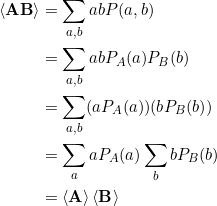
Aufgabe 7.10
Zeigen Sie, dass der Zustandsvektor in Gl. 7.30 einen vollständig unverschränkten Zustand darstellt.
Lösung:
Gemeint ist der Zustand ![]() , wobei
, wobei ![]() der leere Zustand der Messapparatur ist.
der leere Zustand der Messapparatur ist.
Er lässt sich als Produktzustand schreiben:
![]()
und als Produktzustand ist er unverschränkt.
Aufgabe 7.11
Berechnen Sie Alices Dichtematrix für ![]() im „Fast-Singulett-Fall“.
im „Fast-Singulett-Fall“.
Lösung:
Der Zustandsvektor lautet:
![]()
woraus wir ablesen:
![]()
Es folgt:

und damit
![]()
Aufgabe 7.12
Überprüfen Sie die numerischen Werte in jedem Steckbrief.
Lösung:
Hier steht uns einiges an Rechnerei vor. Immerhin habe wir einen wichtigen Teil schon erledigt, denn in Abschnitt 6.8 haben wir die Wirkung der Pauli-Matrizen ![]() bzw.
bzw. ![]() schon einmal berechnet (jedenfalls zum Teil), und im Anhang 5 zusammengefasst. Die für uns wichtige Tabelle A.1 (up-down-Basis) schreiben wir uns hier noch einmal hin:
schon einmal berechnet (jedenfalls zum Teil), und im Anhang 5 zusammengefasst. Die für uns wichtige Tabelle A.1 (up-down-Basis) schreiben wir uns hier noch einmal hin:
| | ||||
| | ||||
Steckbrief 2: Der Singulett-Zustand wurde in Abschnitt 6.9. ausführlich durchgerechnet.
Steckbrief 3: Der Zustandsvektor lautet ![]() .
.
Die Koeffizienten der Dichtematrix erhält man aus:
![Rendered by QuickLaTeX.com \[ \begin{split}\rho_{uu} &= \psi^*_{uu} \psi_{uu} + \psi^*_{ud} \psi_{ud} = 0 + 0,6^2 = 0,36 \\\rho_{ud} &= \psi^*_{uu} \psi_{du} + \psi^*_{ud} \psi_{dd} = 0 + 0 = 0 \\\rho_{du} &= \psi^*_{du} \psi_{uu} + \psi^*_{dd} \psi_{ud} = 0 + 0 = 0 \\\rho_{dd} &= \psi^*_{du} \psi_{du} + \psi^*_{dd} \psi_{dd} = 0,4^2 + 0 = 0,16. \end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-2bf2b55c47821795768ba88ee33a513e_l3.png)
Die Dichtematrix hat also die Gestalt
![]()
Es folgt
![]()
und
![]()
Für die Erwartungswerte gilt:
![Rendered by QuickLaTeX.com \[ \begin{split}\braket{\sigma_z} = \bra{\psi} (\sigma_z \ket{\psi}) &= \bra{\psi} (\sigma_z (\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) ) \\&= \bra{\psi} (\sqrt{0,6} \ket{ud} - (- \sqrt{0,4} \ket{du}))\\ &=(\sqrt{0,6} \bra{ud} - \sqrt{0,4} \bra{du} )(\sqrt{0,6} \ket{ud} - (- \sqrt{0,4} \ket{du})) \\&=\sqrt{0,6}\sqrt{0,6} - \sqrt{0,4} \sqrt{0,4}\\&= 0,2.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-99b85a0c4be9f031ae363e8f3cc1463b_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\braket{\tau_z} = \bra{\psi} (\tau_z \ket{\psi}) &= \bra{\psi} (\tau_z (\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) ) \\&= \bra{\psi} (- \sqrt{0,6} \ket{ud} - ( \sqrt{0,4} \ket{du}))\\&=(\sqrt{0,6} \bra{ud} - \sqrt{0,4} \bra{du} )(-\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) \\&=-\sqrt{0,6}\sqrt{0,6} + \sqrt{0,4} \sqrt{0,4}\\&= -0,2.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-f8398a10d2690577411feedb20ba1013_l3.png)
Da bei der Anwendung von ![]() die Basisvektoren
die Basisvektoren ![]() und
und ![]() auf die Vektoren
auf die Vektoren ![]() und
und ![]() abgebildet werden, ergibt die Anwendung von
abgebildet werden, ergibt die Anwendung von ![]() auf das Ergebnis jeweils 0.
auf das Ergebnis jeweils 0.
Wir zeigen dies am Beispiel von ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split}\braket{\sigma_x} = \bra{\psi} (\sigma_x \ket{\psi}) &= \bra{\psi} (\sigma_x (\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) ) \\&= \bra{\psi} (\sqrt{0,6} \ket{dd} - \sqrt{0,4} \ket{uu})\\&=(\sqrt{0,6} \bra{ud} - \sqrt{0,4} \bra{du} )(\sqrt{0,6} \ket{uu} - \sqrt{0,4} \ket{dd})) \\&= 0.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-ba4374c408ebce05dd419c56a9447dad_l3.png)
Weiter ist
![Rendered by QuickLaTeX.com \[ \begin{split}\braket{\tau_z \sigma_z} = \bra{\psi} (\tau_z \sigma_z \ket{\psi}) &= \bra{\psi} (\tau_z \sigma_z (\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) ) \\&= \bra{\psi} (- \sqrt{0,6} \ket{ud} - ( -\sqrt{0,4} \ket{du}))\\&=(\sqrt{0,6} \bra{ud} - \sqrt{0,4} \bra{du} )(-\sqrt{0,6} \ket{ud} - ( -\sqrt{0,4} \ket{du})) \\&=-\sqrt{0,6}\sqrt{0,6} - \sqrt{0,4} \sqrt{0,4}\\&= -1.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-6d03469793291239c56414b58bf1e1ee_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split}\braket{\tau_x \sigma_x} = \bra{\psi} (\tau_x \sigma_x\ket{\psi}) &= \bra{\psi} (\tau_x \sigma_x (\sqrt{0,6} \ket{ud} - \sqrt{0,4} \ket{du}) ) \\&= \bra{\psi} ( \sqrt{0,6} \ket{du} - \sqrt{0,4} \ket{ud})\\&=(\sqrt{0,6} \bra{ud} - \sqrt{0,4} \bra{du} )(\sqrt{0,6} \ket{du} - \sqrt{0,4} \ket{ud}) \\&=-\sqrt{0,6}\sqrt{0,4} - \sqrt{0,4} \sqrt{0,6}\\&= -2 \sqrt{0,6}\sqrt{0,4} \\ &= -2 \sqrt{0,24}.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-c87503ef28feffea54bbcac93bfe0a85_l3.png)
Für die Korrelation gilt also
![]()

Da steckt ein Fehler in der Aufgabenstellung zu Aufgabe 7.3. b). Die Ergebnisse der Multiplikationen Aa und Bb sind 2 x 1 – Matrizen, wie es ja auch in der Lösung steht.
Vielen Dank für den Hinweis. Habe ich korrigiert!