Lösungen Band I, Vorlesung 7

Aufgabe 7.1

Leiten Sie Gl. 7.2 her, und erklären Sie den Unterschied bei den Vorzeichen.

Lösung:

Es gilt

    \[\dot{p_i} = \frac{dp_i}{dt} = \pd{\Lag}{q_i}.\]


Die Lagrange-Funktion lautet \Lag = \frac{1}{2} (\dot{q}_1^2 + \dot{q}_2^2 ) - V(q_1-q_2), also ist

    \[\begin{split}\dot{p_1} &= \pd{}{q_1} \left(\frac{1}{2} (\dot{q}_1^2 + \dot{q}_2^2 ) - V(q_1-q_2) \right)\\&= - \pd{V(q_1-q_2) }{q_1} \\&= -V'(q_1-q_2) \pd{ (q_1-q_2)}{q_1} = -V'(q_1-q_2)\end{split}\]


und

    \[\begin{split}\dot{p_2} &= \pd{}{q_2} \left(\frac{1}{2} (\dot{q}_1^2 + \dot{q}_2^2 ) - V(q_1-q_2) \right) \\&= - \pd{V(q_1-q_2) }{q_2}\\&= -V'(q_1-q_2) \pd{(q_1-q_2) }{q_2} = V'(q_1-q_2).\end{split}\]


Das unterschiedliche Vorzeichen stammt aus dem Minuszeichen vor q_2 in V(q_1-q_2).

Aufgabe 7.2

Erklären Sie die Erhaltung bp_1 + ap_2

Wie auf Seite 100 in Band I beschrieben, geht es dabei um die Lagrange-Funktion \Lag = \frac{1}{2}(\dot{q}_1^2 + \dot{q}_2^2) - V(aq_1 +bq_2) und die Erhaltung bp_1+ap_2. Die Bewegungsgleichungen lauten

    \[\begin{split}\dot{p}_1 &= -aV'(aq_1-bq_2)\\\dot{p}_2 &= +bV'(aq_1-bq_2)\end{split}\]


(s. S. 100 in Band I)

Lösung:

Multiplizieren wir die erste Bewegungsgleichung mit b und die zweite mit a, so erhalten wir

    \[\begin{split}b \dot{p}_1 &= -abV'(aq_1-bq_2)\\a \dot{p}_2 &= +abV'(aq_1-bq_2).\end{split}\]


Durch Addition der beiden Zeilen erhalten wir b \dot{p}_1 + a \dot{p}_2 = 0, d.h. \frac{d}{dt}(bp_1+ap_2) = 0. bp_1+ap_2 ändert sich also nicht mit der Zeit.

Aufgabe 7.3

Zeigen Sie, dass die Kombination aq_1-bq_2 zusammen mit der Lagrange-Funktion invariant ist unter der Transformation 7.7.

Es geht wieder um die Lagrange-Funktion \Lag = \frac{1}{2}(\dot{q}_1^2 + \dot{q}_2^2) - V(aq_1 +bq_2), und um die Transformation

    \[\begin{split}q_1 &\rightarrow q_1 - b\delta.\\q_2 &\rightarrow q_2 + a\delta.\end{split}\]

Lösung:

Einfaches Einsetzen der Transformation in die Lagrange-Funktion ergibt:

    \[\begin{split}\Lag &= \frac{1}{2}((\frac{d}{dt}(q_1 - b\delta))^2 + (\frac{d}{dt}(q_2 + a\delta))^2) - V(a(q_1- b\delta) +b(q_2 + a\delta))\\&=\frac{1}{2}(\dot{q}_1^2 + \dot{q}_2^2) - V(aq_1 +bq_2 - ab\delta + ba\delta))\\&=\frac{1}{2}(\dot{q}_1^2 + \dot{q}_2^2) - V(aq_1 +bq_2).\end{split}\]


Die Transformation lässt die Lagrange-Funktion also unverändert.

Aufgabe 7.4

Zeigen Sie, dass dies stimmt.

Zu beweisen ist, dass für eine radialsymmetrische Potentialfunktion V die Lagrangefunktion aus Gl. 7.8

    \[ \Lag = \frac{m}{2} (\dot{x}^2 + \dot{y}^2) - V(x^2 + y^2) \]


invariant ist unter der Variation aus Gl. 7.12

    \[\begin{split}\delta_\nu x &= y\delta\\\delta_\nu y &= -x\delta,\end{split}\]


wenn \delta klein ist.

Lösung:

Die Variation aus Gl. 7.12 entspricht der Transformation

    \[\begin{split}x &\rightarrow x +y \delta\\y &\rightarrow y -x \delta.\end{split}\]


Es folgt für die Ableitungen

    \[\begin{split}\dot{x} &\rightarrow \dot{x} + \dot{y} \delta\\\dot{y} &\rightarrow \dot{y} - \dot{x} \delta.\end{split}\]


Damit wird aus

    \[\begin{split}x^2 + y^2 &\rightarrow (x + y\delta)^2 + (y -x \delta)^2\\&= x^2 + 2xy\delta + y^2\delta^2 + y^2 -2xy\delta + x^2\delta^2\\&= \dot{x}^2 + \dot{y}^2 + (x^2 + y^2)\delta^2.\end{split}\]


Entsprechend gilt

    \[\begin{split}\dot{x}^2 + \dot{y}^2 &\rightarrow \frac{d}{dt}(x + y\delta)^2 + \frac{d}{dt}(y -x \delta)^2\\&= \dot{x}^2 + \frac{d}{dt}2xy\delta + \dot{y}^2\delta^2 + \dot{y}^2 -\frac{d}{dt}2xy\delta + \dot{x}^2\delta^2\\&= \dot{x}^2 + \dot{y}^2 + (\dot{x}^2 + \dot{y}^2)\delta^2.\end{split}\]


Es gilt also

    \[\Lag = \frac{m}{2} (\dot{x}^2 + \dot{y}^2 + (\dot{x}^2 + \dot{y}^2)\delta^2) - V(x^2 + y^2 + (\dot{x}^2 + \dot{y}^2)\delta^2) \longrightarrow \frac{m}{2} (\dot{x}^2 + \dot{y}^2) - V(x^2 + y^2).\]


Der letzte Übergang gilt für kleine \delta, da wir dann die Terme zweiter Ordnung (\dot{x}^2 + \dot{y}^2)\delta^2 und (x^2 + y^2)\delta^2 ignorieren können.

Aufgabe 7.5

Bestimmen Sie die Bewegungsgleichungen für ein einfaches Pendel der Länge l, das in der x-y-Ebene mit einem Startwinkel \theta schwingt.

Lösung:

Rendered by QuickLaTeX.com

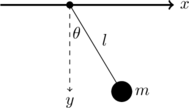
Die Lagrange-Funktion des Pendels ergibt sich aus der Differenz zwischen der kinetischen Energie T und der potentiellen Energie V. Da die Länge des Pendel konstant l beträgt, gibt es nur einen Freiheitsgrad, der durch die generalisierte Koordinate \theta beschrieben wird. Aus der Skizze liest man ab:

    \[\begin{split}x &= l \sin \theta\\y &= l \cos \theta,\end{split}\]


also

    \[\begin{split}\dot{x} &= +l \cos \theta\\\dot{y} &= -l \sin \theta.\end{split}\]


Damit lautet die kinetische Energie (die Masse des Pendels sei m):

    \[ T = \frac{m}{2} (\dot{x}^2 + \dot{y}^2) = \frac{m}{2} l^2(\cos^2 \theta + \sin^2 \theta)\dot{{\theta}} = \frac{ml^2\dot{{\theta}}}{2}. \]


Die potentielle Energie des Pendels ist

    \[ V = m g y = m g l \cos \theta.\]


Die Lagrange-Funktion \Lag ist somit

    \[ \Lag = \frac{ml^2\dot{\theta}}{2} - m g l \cos \theta. \]


Die Bewegungsgleichungen ergeben sich nun aus \frac{d}{dt} \pd{\Lag}{\dot{\theta}} = \pd{\Lag}{\theta}:

    \[\begin{split}\frac{d}{dt} \pd{\Lag}{\dot{\theta}} &= \frac{d}{dt} \pd{\Lag}{\dot{\theta}} = \frac{d}{dt} \pd{}{\dot{\theta}} (\frac{ml^2\dot{\theta}}{2} - m g l \cos \theta) = ml^2 \ddot{\theta},\\\pd{\Lag}{\theta} &= \pd{}{\theta} (\frac{ml^2\dot{\theta}}{2} - m g l \cos \theta) = -mgl\sin \theta,\end{split}\]


also

    \[ ml^2 \ddot{\theta} = -mgl\sin \theta \]


und damit

    \[\ddot{\theta} = -\frac{g}{l} \sin \theta.\]


Das ist die Bewegungsgleichung für ein einfaches Pendel. Zwei Dinge fallen auf:

  • Die Beschleunigung von \theta ist unabhängig von der Masse des Pendels
  • Die Beschleunigung von \theta wird umso kleiner, je größer l ist (lange Pendel schwingen langsam)


Das einfache Pendel ist ein schönes Beispiel für die Lagrange-Methode. Es zeigt auch, dass die Bewegungsgleichungen nicht einfach lösbar sein müssen: Die Differentialgleichung \ddot{\theta} = -\frac{g}{l} \sin \theta hat keine Lösungs-Funktion \theta(t), die man direkt hinschreiben kann. Man kann aber für eine Näherungslösung in der Differentialgleichung die Funktion \sin \theta durch die lineare Näherung \theta(t) ersetzen, was für kleine \theta keinen allzu großen Fehler ergibt. Die neue Differentialgleichung \ddot{\theta} = -\frac{g}{l} \theta hat nun z.B. die Lösung \theta(t) = \sin \sqrt{\frac{g}{l}} t.

Aufgabe 7.6

Bestimmen Sie die Euler-Lagrange-Gleichungen für \theta und \alpha.

Lösung:

Gemeint sind hierbei die beiden Winkel beim Doppelpendel wie in der folgenden Skizze:

Rendered by QuickLaTeX.com

Dabei sind der Einfachheit halber M_1 = M_2 = 1 und r_1 = r_2 = 1.

Die Lagrange-Funktion lautet:

    \[ \Lag = \frac{\dot{\theta}^2}{2} + \dfrac{\dot{\theta}^2 + (\dot{\theta} + \dot{\alpha})^2}{2} + \dot{\theta}(\dot{\theta} + \dot{\alpha})\cos \alpha + g [2 \cos \theta + \cos (\theta + \alpha)].\]


Dabei stammt der letzte Term mit dem führenden g aus den Potential der Schwerkraft. Wir erhalten aus \Lag zwei Bewegungsgleichungen für \theta und \alpha aus den Euler-Lagrange-Gleichungen:

    \begin{align*}\frac{d}{dt}\pd{\Lag}{\dot{\theta}} &= \frac{d}{dt} \big[ \dot{\theta} + \dot{\theta} + (\dot{\theta} + \dot{\alpha}) + \cos(\alpha)((\dot{\theta} + \dot{\alpha}) + \dot{\theta}) \big]\\&= 3 \ddot{\theta} + \ddot{\alpha} - \dot{\alpha} (2\dot{\theta} + \dot{\alpha})\sin(\alpha ) + (2 \ddot{\theta} + \ddot{\alpha})\cos(\alpha), \\\pd{\Lag}{\theta} &= g \big[ -2 \sin \theta - \sin (\theta + \alpha) \big] = -g \big[ 2 \sin \theta + \sin (\theta + \alpha) \big].\end{align*}

und

    \begin{align*}\frac{d}{dt}\pd{\Lag}{\dot{\alpha}} &= \frac{d}{dt} \big[ (\dot{\theta} + \dot{\alpha}) + \cos(\alpha) - \dot{\theta}(\dot{\theta} + \dot{\alpha}) \sin \alpha \big]\\&= \ddot{\theta} + \ddot{\alpha} -\dot{\alpha} \sin \alpha - (2 \dot{\theta} \ddot{\theta} - \dot{\theta} + \ddot{\theta} \dot{\alpha} + \dot{\theta} \ddot{\alpha}) \sin \alpha - \dot{\theta}\dot{\alpha}(\dot{\theta} + \dot{\alpha}) \cos \alpha , \\ \pd{\Lag}{\alpha} &= -g \sin(\theta + \alpha).\end{align*}

Die Bewegungsgleichungen lauten damit:

    \begin{align*}3 \ddot{\theta} + \ddot{\alpha} - \dot{\alpha} (2\dot{\theta} + \dot{\alpha})\sin(\alpha ) + (2 \ddot{\theta} + \ddot{\alpha})\cos(\alpha) + g \big[ 2 \sin \theta + \sin (\theta + \alpha)\big] = 0\\\ddot{\theta} + \ddot{\alpha} -\dot{\alpha} \sin \alpha - (2 \dot{\theta} \ddot{\theta} - \dot{\theta} + \ddot{\theta} \dot{\alpha} + \dot{\theta} \ddot{\alpha}) \sin \alpha - \dot{\theta}\dot{\alpha}(\dot{\theta} + \dot{\alpha}) \cos \alpha + g \sin(\theta + \alpha) = 0\end{align*}

Bei solchen Differentialgleichungen besteht keine Hoffnung auf exakte Lösungen, hier kommen dann numerische Verfahren zur Annäherung von Lösungen zum Einsatz. Ein großes Problem ist auch, dass die Funktionen \theta und \alpha samt ihren Ableitungen in beiden Gleichungen auftauchen. Solche Differentialgleichungen werden gekoppelt genannt, was natürlich der mechanischen Kopplung der beiden Pendel entspricht. Man kann die beiden Gleichungen also nicht nacheinander, sondern nur gleichzeitig lösen.

Aufgabe 7.7

Leiten Sie die Formel für den Drehimpuls des Doppelpendels her, und beweisen Sie, dass er bei fehlendem Gravitationsfeld erhalten bleibt.

Lösung:

In Aufgabe 7.6 haben wir bereits die zu \theta und \alpha konjugieren Impulse berechnet:

    \begin{align*} p_\theta &= \pd{\Lag}{\theta} = 3 \dot{\theta} + \dot{\alpha} + (2\dot{\theta} + \dot{\alpha}) \cos\alpha \\ p_\alpha &= \pd{\Lag}{\alpha} = \dot{\theta} + \dot{\alpha} + \cos(\alpha) - \dot{\theta}(\dot{\theta} + \dot{\alpha}) \sin \alpha. \end{align*}


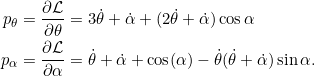
Bei fehlender Schwerkraft entfällt in den Bewegungsgleichungen das Gravitationspotential, so dass \theta und \alpha zyklische Variablen sind und somit gilt

    \begin{align*} p_\theta &= \pd{\Lag}{\dot{\theta}} = 3 \dot{\theta} + \dot{\alpha} + (2\dot{\theta} + \dot{\alpha}) \cos\alpha = \text{const}\\p_\alpha &= \pd{\Lag}{\dot{\alpha}} = \dot{\theta} + \dot{\alpha} + \cos(\alpha) - \dot{\theta}(\dot{\theta} + \dot{\alpha}) \sin \alpha = \text{const}. \end{align*}

3 Kommentare

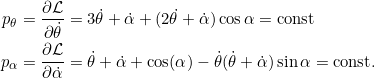
  1. Hallo Herr Sippel,

    Aufgabe 7.4. kann auch, so übersetzen Sie, durch einfache Analysis gelöst werden. Diese Lösung wollte ich hier ergänzen.

    Ansatz: In erster Näherung gilt:

    f(x+∆x, y+∆y) = f(x,y) + ∆x mal ∂f/∂x + ∆y mal ∂f/∂y bzw.

    f(x+∆x, y+∆y) – f(x,y) = ∆x mal ∂f/∂x + ∆y mal ∂f/∂y

    Das sind die ersten beiden Glieder der Taylorreihe, das ergibt sich aber auch aus der Definition der Ableitung df/dx = (f(x+∆x)-f(x))/∆x durch Umstellen.

    Damit gilt in erster Näherung für die Variation der Lagrange-Funktion (die bezeichne ich mit D, da das klein-Delta-Symbol auf der Tastatur fehlt, für x-Punkt und y-Punkt schreibe ich aus demselben Grund x´ und y´):

    DL = L(x+∆x, y+∆y, x´+∆x´, y´+∆y´) – L(x,y,x´,y´) = Dx mal ∂L/∂x + Dy mal ∂L/∂y + Dx´ mal ∂L/∂x´ + Dy´ mal ∂L/∂y´ ,

    und die soll null sein. Also, da Dx=yD und Dy=-xD

    DL = yD mal ∂L/∂x – xD mal ∂L/∂y + y´D mal ∂L/∂x´ – x´D mal ∂L/∂y´= 0

    Das geht einfach auszurechnen (der Ansatz ist das Schwierige!) und ergibt:

    DL = – dV/d(x^2 + y^2) mal 2x mal Dy – dV/d(x^2 + y^2) mal 2y mal (-Dx)

    (ist bis hierhin schonmal null)

    + y´D mal x´ – x´D mal y´ = 0

    Die Lagrange-Funktion ändert sich also in erster Näherung nicht, DL=0, wenn x und y in Rotationsrichtung um Dy bzw. – DX verschoben werden.

    Hat Spaß gemacht, das selbst rauszufinden.

    Viele Grüße, Frank Gilewitz

    Antworten

  2. Hallo Herr Sippel,

    ich glaube, in der Lösung zu 7.6 fehlen in den partiellen Ableitungen jeweils die Punkte über Theta und Alpha. Die konjungierten Impulse ergeben sich aus den partiellen Ableitungn nach Theta-Punkt und Alpha-Punkt, (so zumindest auf Seite 96 dargestellt). Vielleicht können Sie einmal nachgucken.
    Viele Grüße, Chris

    Antworten

Hinterlasse einen Kommentar.

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert