Lösungen Band II, Vorlesung 2

Aufgabe 2.1

Beweisen Sie, dass der Vektor \ket{r} in Gl. 2.5 orthogonal auf dem Vektor \ket{l} in Gl. 2.6 steht.

Lösung:

    \begin{align*}\ket{r} &= \frac{1}{\sqrt{2}} \ket{u} + \frac{1}{\sqrt{2}} \ket{d}\;\;\;\;\;\;\;\;\;(2.5) \\\ket{l} &= \frac{1}{\sqrt{2}} \ket{u} - \frac{1}{\sqrt{2}} \ket{d}\;\;\;\;\;\;\;\;\;(2.6)\end{align*}

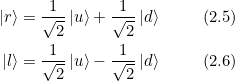
Es ist damit

    \begin{align*}\braket{l|r} &= \frac{1}{\sqrt{2}} \big(\bra{u} - \bra{d} \big) \frac{1}{\sqrt{2}} \big(\ket{u} + \ket{d} \big)\\&= \frac{1}{2}\big( \braket{u|u} + \braket{u|d} - \braket{d|u} - \braket{d|d} \big)\\&= \frac{1}{2} \big( 1 + 0 - 0 - 1\big)\\&= 0.\end{align*}


\ket{l} und \ket{r} stehen also senkrecht aufeinander.

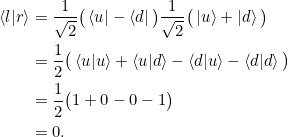
Aufgabe 2.2

Beweisen Sie, dass \ket{i} und \ket{o} alle Bedingungen aus den Gleichungen 2.7, 2.8 und 2.9 erfüllen. Sind sie dadurch eindeutig bestimmt?

Lösung:

Das ist nun einmal wirklich reine Fleißarbeit. Es sind

    \begin{align*}\ket{i} &= \frac{1}{\sqrt{2}} \ket{u} + \frac{i}{\sqrt{2}} \ket{d} \Longrightarrow \bra{i} = \frac{1}{\sqrt{2}} \bra{u} - \frac{i}{\sqrt{2}} \bra{d},\\\ket{o} &= \frac{1}{\sqrt{2}} \ket{u} - \frac{i}{\sqrt{2}} \ket{d} \Longrightarrow \bra{o} = \frac{1}{\sqrt{2}} \bra{u} + \frac{i}{\sqrt{2}} \bra{d}.\end{align*}

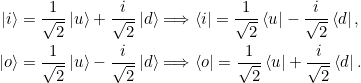
Gleichungen 2.7 (Orthogonalität)


    \begin{align*}\braket{i|o} &= \frac{1}{\sqrt{2}} \big(\bra{u} - i\bra{d} \big) \frac{1}{\sqrt{2}} \big(\ket{u} - i \ket{d} \big)\\&= \frac{1}{2} \big( \braket{u|u} - i \braket{u|d} - i \braket{d|u} + i^2\braket{d|d} \big)\\&= \frac{1}{2} \big(1 - 0 - 0 - 1\big)\\&= 0.\end{align*}

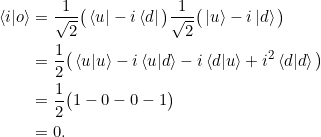
Gleichungen 2.8

Wir berechnen die Produkte mit \ket{u} und \ket{d}:

    \begin{align*}\braket{o|u} &= \frac{1}{\sqrt{2}}\big(\bra{u} + i \bra{d} \big) \ket{u} = \frac{1}{\sqrt{2}} (\braket{u|u} + i \braket{d|u}) = \frac{1}{\sqrt{2}},\\\braket{i|u} &= \frac{1}{\sqrt{2}}\big(\bra{u} - i \bra{d} \big) \ket{u} = \frac{1}{\sqrt{2}} (\braket{u|u} - i \braket{d|u}) = \frac{1}{\sqrt{2}},\\\braket{o|d} &= \frac{1}{\sqrt{2}}\big(\bra{u} + i \bra{d} \big) \ket{d} = \frac{1}{\sqrt{2}} (\braket{u|d} + i \braket{d|d}) = \frac{+i}{\sqrt{2}},\\\braket{i|d} &= \frac{1}{\sqrt{2}}\big(\bra{u} - i \bra{d} \big) \ket{d} = \frac{1}{\sqrt{2}} (\braket{u|d} - i \braket{d|d}) = \frac{-i}{\sqrt{2}}.\end{align*}

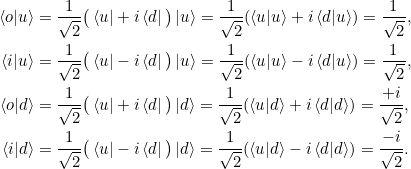
Wenn wir nun die Antisymmetrie verwenden, so sehen wir die Gleichungen aus 2.8:

    \begin{align*}\braket{o|u}\braket{u|o} &= \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}} = \frac{1}{2},\\\braket{i|u} \braket{u|i}&= \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}} = \frac{1}{2},\\\braket{o|d} \braket{d|o} &= \frac{+i}{\sqrt{2}} \frac{-i}{\sqrt{2}}=\frac{1}{2},\\\braket{i|d}\braket{d|i} &= \frac{-i}{\sqrt{2}} \frac{+i}{\sqrt{2}}=\frac{1}{2}.\end{align*}

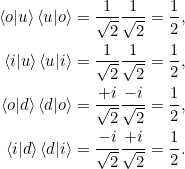
Gleichungen 2.9

Es sind \ket{l} = \frac{1}{\sqrt{2}}(\ket{u} + \ket{d}) und \ket{r}= \frac{1}{\sqrt{2}}(\ket{u} - \ket{d}. Mittlerweile sehen wir, wie das läuft: Die gemischten Terme fallen weg wegen \braket{u|d} = \braket{d|u}=0, und übrig bleiben die Terme \braket{u|u} = \braket{d|d}=1:

    \begin{align*}\braket{o|r} &= \frac{1}{\sqrt{2}}\big(\bra{u} + i \bra{d} \big) \frac{1}{\sqrt{2}}(\ket{u} + \ket{d}) = \frac{1-i}{2},\\\braket{o|l} &= \frac{1}{\sqrt{2}}\big(\bra{u} + i \bra{d} \big) \frac{1}{\sqrt{2}}(\ket{u} - \ket{d})= \frac{1+i}{2},\\\braket{i|r} &= \frac{1}{\sqrt{2}}\big(\bra{u} - i \bra{d} \big) \frac{1}{\sqrt{2}}(\ket{u} + \ket{d})= \frac{1+i}{2},\\\braket{i|l} &= \frac{1}{\sqrt{2}}\big(\bra{u} - i \bra{d} \big) \frac{1}{\sqrt{2}}(\ket{u} - \ket{d}) = \frac{1-i}{2}.\end{align*}

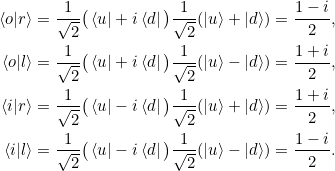
und damit wegen der Antisymmetrie \braket{A,B} = \braket{B,A}^* und (1+i)(1-i) = 1 - i^2=2:

    \begin{align*}\braket{o|r}\braket{r|o} &= \frac{1-i}{2} \frac{1+i}{2}= \frac{2}{4} = \frac{1}{2},\\\braket{o|l} \braket{l|o} &= \frac{1+i}{2} \frac{1-i}{2}= \frac{2}{4}=\frac{1}{2},\\\braket{i|r} \braket{r|i}&= \frac{1+i}{2} \frac{1-i}{2}= \frac{2}{4} = \frac{1}{2},\\\braket{i|l}\braket{l|i} &= \frac{1-i}{2} \frac{1+i}{2}= \frac{2}{4}=\frac{1}{2}.\end{align*}

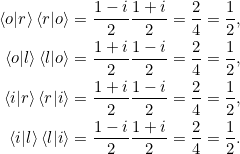
Auf die Frage nach der eindeutigen Bestimmtheit gehen wir in Aufgabe 2.3 ein.

Aufgabe 2.3

Vergessen wir einmal, dass uns die Gleichungen 2.10 funktionierende Definitionen für \ket{i} und \ket{o} ausgedrückt in Termen von \ket{u} und \ket{d} geben, und nehmen wir an, die Komponenten \alpha, \beta, \gamma und \delta seien noch unbekannt:

    \begin{align*}\ket{i} &= \alpha \ket{u} + \beta \ket{d}\\\ket{o} &= \gamma \ket{u} + \delta \ket{d}.\end{align*}



a) Zeigen Sie mit Hilfe der Gleichungen 2.8, dass gilt

    \[\alpha^* \alpha = \beta^* \beta = \gamma^* \gamma = \delta^* \delta = \frac{1}{2}.\]


b) Zeigen Sie mit dem ersten Resultat und den Gleichungen 2.9, dass gilt

    \[\alpha^* \beta + \alpha \beta^* = \gamma^* \delta + \gamma \delta^* = 0.\]


c) Zeigen Sie, dass \alpha^* \beta und \gamma^* \delta rein imaginär sein müssen.
Ist \alpha^* \beta rein imaginär, so können \alpha und \beta nicht beide reell sein. Dasselbe gilt für \gamma und \delta.

Lösung:

Im Aufgabentext haben wir den allgemeinen Ansatz für \ket{i} und \ket{o}, ausgedrückt in der \ket{u}–\ket{d}-Basis. Wir wollen nun zeigen, wie weit \alpha, \beta, \gamma, \delta durch die Produkte mit den anderen Zustandsvektoren bestimmt sind.

a) Die Produkte mit \ket{u} und \ket{d}:

Es ist nach Gl. 2.8

    \[ \frac{1}{2} = \braket{i|u}\braket{u|i} = \big(\alpha^* \braket{u|u} + \beta^* \braket{d|u}\big)\big(\alpha \braket{u|u} + \beta \braket{u|d}\big) = \alpha^*\alpha.\]


    \[ \frac{1}{2} = \braket{i|d}\braket{d|i} = \big(\alpha^* \braket{u|d} + \beta^* \braket{d|d}\big)\big(\alpha \braket{d|u} + \beta \braket{d|d}\big) = \beta^*\beta.\]


Genau so folgen die Gleichungen \gamma^*\gamma = \frac{1}{2} und \delta^*\delta = \frac{1}{2}.

b) Es ist

    \[ \braket{i|r} = \big(\alpha^* \bra{u} + \beta^* \bra{d}\big) \frac{1}{\sqrt{2}}(\ket{u} + \ket{d}) = \frac{1}{\sqrt{2}}(\alpha^* + \beta^*).\]

Es folgt \braket{r|i} = \frac{1}{\sqrt{2}}(\alpha + \beta), also gilt

    \[ \frac{1}{2} = \braket{i|r} \braket{r|i} = \frac{1}{2} \big( (\alpha^* + \beta^*) (\alpha + \beta) \big) = \frac{1}{2} \big( \alpha^*\alpha + \beta^*\beta + \alpha^*\beta + \alpha \beta^*. \big), \]

also

    \[ \alpha^*\alpha + \beta^*\beta + \alpha^*\beta + \alpha \beta^* = 1.\]

Aus a) wissen wir \alpha^*\alpha + \beta^*\beta = \frac{1}{2} + \frac{1}{2} = 1, d.h es muss gelten

    \[ \alpha^*\beta + \alpha \beta^* = 0. \]


Mit dem Produkt \braket{o|r}\braket{r|o} = \frac{1}{2} folgt auf dieselbe Weise \gamma^*\delta + \gamma \delta^* = 0.

c) Aus den Gleichungen in b) folgt, dass \alpha^*\beta rein imaginär ist, denn es gilt


    \[ \alpha^*\beta + \alpha\beta^* = 0 \Longrightarrow \alpha^*\beta = -\alpha\beta^* = (-\alpha^*\beta)^*,\]


d.h. die konjugiert komplexe Zahl von \alpha^*\beta ist -\alpha^*\beta.

Der Realteil von \alpha^*\beta ist daher 0, und damit ist \alpha^*\beta rein imaginär. Das gleiche gilt für \gamma^*\delta.

6 Kommentare

  1. Kann es sein, dass sich in die Lösung von 2.3 b) ein Fehler eingeschlichen hat? Wenn man (α*+β*)(α+β) ausmultipliziert, so erhält man meiner Meinung nach α*α+β*β+α*β+αβ*, wie es auch in der vorletzten Zeile des Beweises steht, und nicht α*+α+β*+β+α*β+αβ*, wie es in am Ende der Gleichungskette darüber heißt.

    Antworten

  2. Aufgabe 2.3, b):
    Kann es sein, dass |l> = (1/sqrt(2))*( |u> – |d>) ist und nicht |l> = (1/sqrt(2))*( |u> + |d>)?
    So steht es zumindest im Buch auf Seite 42 oben.

    Antworten

    1. Hallo Dustin,
      stimmt, ich habe hier |l> mit |r> verwechselt, so wie sie in Gl. 2.5 und 2.6 definiert sind. Die Rechnung und Argumentation funktioniert also richtig mit |r>. Das habe ich auch korrigiert. Man beachte aber, dass die Definitionen von |l> und |r> insofern willkürlich sind, als man sie auch „andersherum“ bezeichnen könnte.

      Antworten

  3. Hallo Herr Sippel,

    zu Aufgabe 2.2. alle Lösungen hätte ich folgende Anmerkung:

    M.E. gehört gemäß Seite 19 Ziffer 2 zum

    i-Ket=1/sqrt2 mal u-Ket + i/sqrt2 mal d-Ket
    der
    i-Bra=u-Bra mal 1/sqrt2 – d-Bra mal i/sqrt2 (also minus statt plus in der Mitte)

    und zum

    o-Ket=1/sqrt2 mal u-Ket – i/sqrt2 mal d-Ket
    der
    o-Bra=u-Bra mal 1/sqrt2 + d-Bra mal i/sqrt2 (also plus statt minus in der Mitte),

    weil mit Z=i/sqrt2 gilt:
    Z-Stern=-i/sqrt2
    und umgekehrt.

    Dann ergeben sich immer noch die richtigen Lösungen, aber mit einsehbarem Lösungsweg, besonders, was Gleichung 2.7. angeht.

    Richtig?

    Viele Grüße, Frank Gilewitz

    Antworten

Hinterlasse einen Kommentar.

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert